In this tutorial, we will learn about merge sort tree java i.e. what is merge sort in java. In merge sort, we divide the unsorted array into n subarrays, each of size one, which can be considered sorted trivially. Then, we repeatedly merge the sorted subarrays to produce new sorted subarrays until there is only one sorted array of size n remaining.
i.e. what is merge sort in java. In merge sort, we divide the unsorted array into n subarrays, each of size one, which can be considered sorted trivially. Then, we repeatedly merge the sorted subarrays to produce new sorted subarrays until there is only one sorted array of size n remaining.
Merge sort is a sorting algorithm that follows the divide and conquers method. we use sorting techniques to rearrange a list of elements into a sorted list, either ascending or descending depending on the requirement. Java merge sort algorithm for array of objects. The default sorting is done in ascending order. We divide the elements into two halves, make the required steps for the two halves separately, and then we merge the two halves. The two halves are:
Divide: We divide the array into two halves and selected the middle element as out pivot element. We carry out this step till we divide the whole half array into little half arrays.
Conquer: We sort the halves of the array. We will then merge the divided arrays.
We can say merge sort is performed as merge(arr, a, m, r) that assumes arr(a,…m) and arr[m+1….r] are in the sorted form then merging two sorted set of elements into one set. For example, we have a list of elements:
23, 10, 62, 25Step 1: we will divide the above set of 4 elements into 2. The first set becomes 23, 10 and second set becomes 62, 25
Step 2: First we check if the first half is sorted. It is not; therefore we swap both the elements. Now we get the first set as 10, 23
Step 3: Now we check if the second half is sorted or not. It is not; therefore we swap both the elements. Now we get the second set as 25, 62
When we merge both the sets using these 3 steps, we get the sorted list of elements as:
10, 23, 25, 62.
It is a sorted set completelyMerge Sort Algorithm
- Find middle point to divide the array into two.
Middle m = (a+r)/2
- Call mergeSort for first half after division
Call mergeSort (arr, a, m)
- It Calls mergeSort for second half
Call mergeSort (arr, m+1, r)
- Merge the two halves sorted in step 2 and step 3.
Call mergeSort(arr, a, m, r)
Merge sort Pseudocode
function mergesort(arr, start, end)
if start = end
return
mid = (start + end) / 2
mergesort(arr, start, mid)
mergesort(arr, mid + 1, end)
merge(arr, start, mid, end)
end function
function merge(arr, start, mid, end)
result :- empty list
i = start
j = mid + 1
while (i <= mid and j <= end)
if (arr[i] <= arr[j])
append arr[i] to result
i = i + 1
else
append arr[j] to result
j = j + 1
end if
end while
while (i <= mid)
append arr[i] to result
i = i + 1
end while
while (j <= end)
append arr[j] to result
j = j + 1
end while
i = start
while(i <= end)
arr[i] = first(result)
i = i + 1
result = rest(result)
end while
end function
Merge Sort Code
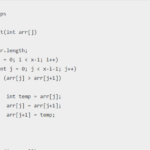
public class DeveloperHelps {
void merge(int arr[], int beg, int mid, int end) {
int l = mid - beg + 1;
int r = end - mid;
int LeftArray[] = new int[l];
int RightArray[] = new int[r];
for (int i = 0; i < l; ++i)
LeftArray[i] = arr[beg + i];
for (int j = 0; j < r; ++j)
RightArray[j] = arr[mid + 1 + j];
int i = 0, j = 0;
int k = beg;
while (i < l && j < r) {
if (LeftArray[i] <= RightArray[j]) {
arr[k] = LeftArray[i];
i++;
} else {
arr[k] = RightArray[j];
j++;
}
k++;
}
while (i < l) {
arr[k] = LeftArray[i];
i++;
k++;
}
while (j < r) {
arr[k] = RightArray[j];
j++;
k++;
}
}
void sort(int arr[], int beg, int end) {
if (beg < end) {
int mid = (beg + end) / 2;
sort(arr, beg, mid);
sort(arr, mid + 1, end);
merge(arr, beg, mid, end);
}
}
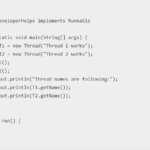
public static void main(String args[]) {
int arr[] = { 23, 51, 22, 45, 1, 4, 90, 29, 17, 55 };
DeveloperHelps ob = new DeveloperHelps();
ob.sort(arr, 0, arr.length - 1);
System.out.println("Sorted array using merge sort is:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
Output :
Sorted array suing merge sort is
1
4
17
22
23
29
45
51
55
90Merge Sort Complexities
- We use it for sorting linked lists. Linked nodes may not be located adjacent in the memory in case of linked lists. We can insert extra elements in O(1) space in O(1) time. Hence we can implement the sorting technique without using that extra space in the linked lists
- We use the algorithm in the inversion count problem.
- The algorithm can also be used in external sorting.
Time Complexity:
Worst case = Average Case = Best Case = O(n log n)
Merge sort performs the same number of operations for any input array of a given size.
In this algorithm, we keep dividing the array into two subarrays recursively which will create O(log n) rows where each element is present in each row exactly once.
For each row, it takes O(n) time to merge every pair of subarrays. So the overall time complexity becomes O(n log n).
Space Complexity:
Since we use an auxiliary array of size at most n to store the merged subarray, the space complexity is O(n)