Selection Sort Algorithm

Selection sort is a selection process to find the smallest element repeatedly from the list of elements is kept. We find the smallest number and keep it in the beginning. The algorithm of selection sort maintains two types of arrays which are:

Two sub-arrays are maintained for selection sort:

• Sorted sub-array: In every iteration, the minimum element is found and placed in its proper position. This sub-array is sorted.
• Unsorted sub-array: The remaining elements that are not sorted.

The selection sort is a straightforward and easy sorting technique. The technique only involves finding the smallest element in every pass and placing it in the correct position. The selection sort is ideal for smaller data sets as it sorts the smaller dataset efficiently.

Selection sort, also known as the in-place sorting algorithm (since it does not require any extra space for sorting) is a sorting algorithm that works on the idea of repeatedly finding the smallest/largest element and placing it at its correct sorted position by swapping it with the element that is currently placed there

We take the smallest element from the unsorted list of elements in each iteration. It is then moved to the list which is sorted. Below is an example of how we can follow iterations for selection sort algorithm:

Read Core Java Interview Questions

Step 1: We have an array of 4 elements arr[0,3]:

23, 56, 11, 27

Step 2: We find the smallest element and we move it to the beginning. The smallest element is 11 so we move it.

The array becomes:

11, 56, 23, 27

Step 3: now we find the next smallest element after 11 which is 23 in the array.

Move 23 in the array of sorted elements. The array becomes:

11, 23, 56, 27

Step 4: in the similar way when we check the next smallest element after 23, it is 27. So we move it to the list of sorted elements.

11, 23, 27, 56

As we check we get the sorted list of elements.

So the list becomes: arr[11, 23, 27, 56]

Selection Sort Algorithm

Java selection Sort algorithm is as follows :

Selection Sort (A, N)

Step 1: Repeat Steps 2 and 3 for K = 1 to N-1

Step 2: Call routine smallest(A, K, N, POS)

Step 3:

Swap A[K] with A [POS]
[End of loop]

Step 4: EXIT

Routine smallest (A, K, N, POS)

Step 1: [initialize] set smallestItem = A[K]

Step 2: [initialize] set POS = K

Step 3:

for J = K+1 to N -1, repeat
if smallestItem > A [J]
set smallestItem = A [J]
set POS = J
[if end]
[End of loop]

Step 4: return POS

As you can see, the routine to find the smallest number is called while traversing the data set. Once the smallest element is found, it is placed in its desired position.

To write an algorithm for the above sorting process, check the steps below:

• Set MIN to 0 location and place it in arr[0].
• Search the smallest element in the list
• Swap the smallest element with the original location of MIN
• Increment MIN to move to the next element.
• Repeat these steps till the list is sorted.

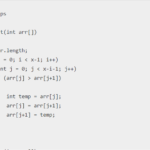
Selection Sort Program in Java

import java.util.Arrays;
public class SelectionSort {
    public static void main(String[] args) {
        int[] arr = {64, 34, 25, 12, 22, 11, 90};
        System.out.println("Original Array: " + Arrays.toString(arr));
        selectionSort(arr);
        System.out.println("Sorted Array: " + Arrays.toString(arr));
    }

    public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            int temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
    }
}

Run Code >>

Output :

Original Array: [64, 34, 25, 12, 22, 11, 90]
Sorted Array: [11, 12, 22, 25, 34, 64, 90]

Complexities :

• Time Complexity : As we can see that, there are two nested for loops, each of which can run for O(n) time. Also, it can be noticed that in every case (iteration of the outer loop), the inner loop will run for n times (or for the remaining number of elements), and hence the time complexity `of selection sort in java in the best case, worst case, and the average case is O(n2).
• Space Complexity : We are not using any extra space to sort the array hence we can say the space complexity of selection sort in java is O(1).

So overall the best and average time complexity of this algorithm is (n^2) and the worst time complexity is O(n^2). However, the space complexity is O(1).

https://www.facebook.com/