Bubble sort in Java - Developer Helps

In this tutorial, we will learn that what is bubble sort in java and how it works. Let’s start

A sorting algorithm can be defined as an algorithm or a procedure to put elements of a collection in a specific order. For instance, if you have a numeric collection like an ArrayList of integers, then you might want to arrange the elements of ArrayList in ascending or descending order.

Similarly, you might want to arrange strings of a string collection in alphabetical or lexicographical order. This is where the sorting algorithms in Java come into the picture.

Bubble sort is the simplest of all sorting techniques in Java. This technique sorts the collection by repeatedly comparing two adjacent elements and swapping them if they are not in the desired order. Thus, at the end of the iteration, the heaviest element gets bubbled up to claim its rightful position.

If there are n elements in list A given by A[0],A[1],A[2],A[3],….A[n-1], then A[0] is compared to A[1], A[1] is compared to A[2] and so on. After comparing if the first element is greater than the second, then the two elements are swapped if they are not in order.

There are many algorithms in java which perform this rearrangement such as java bubble sort, bucket sort, merge sort, radix sort, insertion sort, selection sort, heap sort, quick sort, counting sort, comb sort etc. Java Bubble sorting is one of the simplest sorting algorithms amongst all these. We will traverse the array from the first elements to the last element In this algorithm. we will put the current element in comparison with the next element and swap both if the current one is greater than the next element.

Here is a step wise process of how bubble sort is performed; say we have to sort the list in ascending order

Step 1: we take a list of unsorted elements or an array

For example the list is: 16, 43, 22,78

Step 2: bubble sort takes the first 2 elements 16, 43 and will check for the bigger elements. In this case, 43 is the bigger one and they are already in the sorted locations so the pointer will move forward.

Step 3: now we compare 43 and 22 where 22 is smaller than 43 so the positions will be swapped. Now the list becomes 16, 22, 43, 78

Step 4: As we compare 43 and 78 now, it is again in the sorted fashion and doesn’t require to be swapped.

Step 5: As a result, we get out final list of sorted elements: 16, 22, 43,78

Algorithm for Bubble Sort

Step 1: For i = 0 to N-1 repeat Step 2

Step 2: For J = i + 1 to N – I repeat

Step 3: if A[J] > A[i]
Swap A[J] and A[i]
[End of Inner for loop]
[End if Outer for loop]

Step 4: Exit

Bubble Sort Pseudocode

Bubble sort is a simple algorithm — the pseudocode for it is also pretty simple and short.

Have a look and use it to write your code in a programming language of your choice.

bubbleSort(array, size)
    for i ← 0 to size - 2
        for j ← 0 to size - 2 - i
            If array[j] and array[j + 1] are not in the correct order
                Swap array[j] with array[j + 1]

Bubble Sort Program code

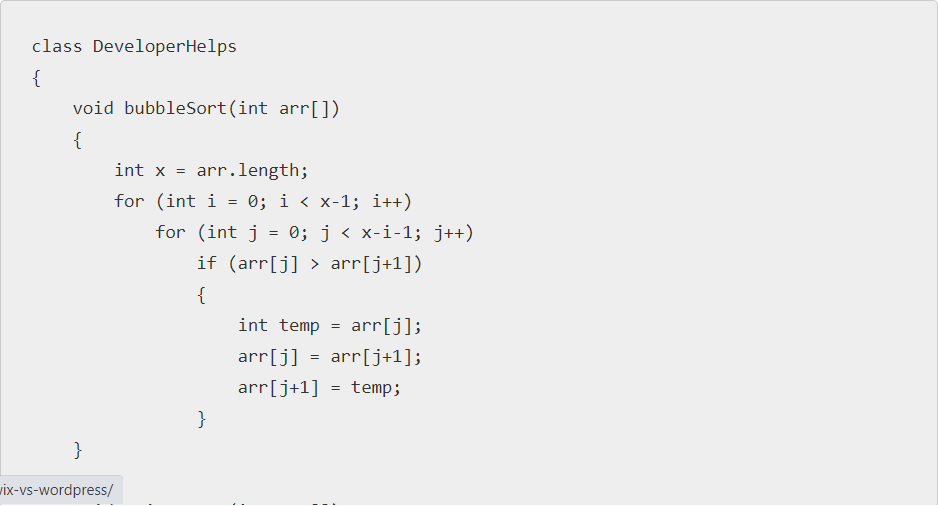
public class DeveloperHelps
{
    void bubbleSort(int arr[])
    {
        int x = arr.length;
        for (int i = 0; i < x-1; i++)
            for (int j = 0; j < x-i-1; j++)
                if (arr[j] > arr[j+1])
                {
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
    }
 
    void printArray(int arr[])
    {
        int x = arr.length;
        for (int i=0; i<x; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
 
    public static void main(String args[])
    {
        DeveloperHelps obj = new DeveloperHelps();
        int arr[] = {100, 300, 200, 500, 220, 601, 90};
        obj.bubbleSort(arr);
        System.out.println("The sorted array via bubble sort algorithm is");
        obj.printArray(arr);
    }
}

Output :

The sorted array via bubble sort algorithm is 
90, 100, 200, 220, 300, 500, 601

Complexities of Bubble Sort

In bubble sort, we compare each adjacent pair. If they are not in the correct order, we swap them. We keep repeating the previous step until no swaps are needed, which indicates all the elements are sorted.

Time Complexity

Worse case: O(n2)

When the array is reverse-sorted, we iterate through the array (n – 1) times. In the first iteration, we do (n – 1) swaps, (n – 2) in the second, and so on until in the last iteration where we do only one swap. Thus the total number of swaps sum up to n * (n – 1) / 2.

Average case: O(n2)

For a completely random array, the total number of swaps averages out to be around n2 / 4, which is again O(n2).

Best case: O(n)

In the first iteration of the array, if we do not perform any swap, we know that the array is already sorted so stop sorting, therefore the time complexity turns out to be linear