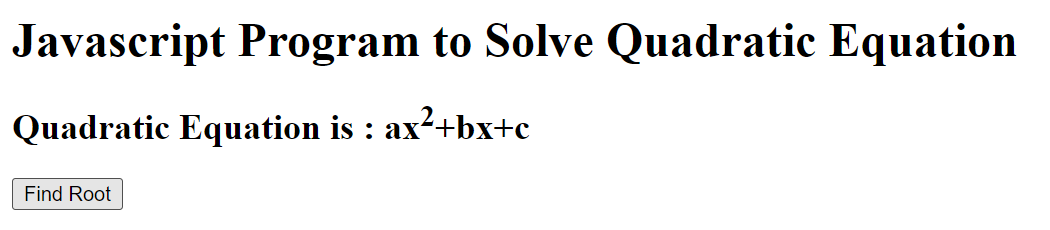In this article, we will see a JavaScript program to Solve Quadratic Equations and for this purpose, we must know what is Quadratic Equation.
The standard form of the quadratic equation:
ax2+bx+c = 0,
a ≠ 0Here a, b and c are coefficient (real number) which is entered by the user. Point to remember that value of ‘a’ can not be zero.
Formula to find the root of the equation:
Every quadratic equation has two roots. Let, these roots are x and y. Then the formula is:
(x,y) = (-b ± √b2-4ac)/2Check out My Latest post on Developer Helps for some Interesting Insights
↠ How to Remove the First Character From String in JavaScript?
↠ How to Remove Duplicates Elements from an Array in JavaScript?
↠ What is the Double Question Mark in JavaScript?




The nature of a root depends upon the discriminant of a quadratic equation i.e. b2-4ac. b2-4ac is knowns as the discriminant of a quadratic equation.
- If the discriminant is greater than 0, the roots are real and different.
- If the discriminant is equal to 0, the roots are real and equal.
- If the discriminant is less than 0, the roots are complex and different.
Let’s see a Javascript Program to Solve Quadratic equations.
<html>
<head>
<title>Quadratic Equation</title>
</head>
<body>
<h1>Javascript Program to Solve Quadratic Equation</h1>
<h2>Quadratic Equation is : ax<sup>2</sup>+bx+c</h2>
<input type = "button" value="Find Root" onclick="func()">
<script>
function func() {
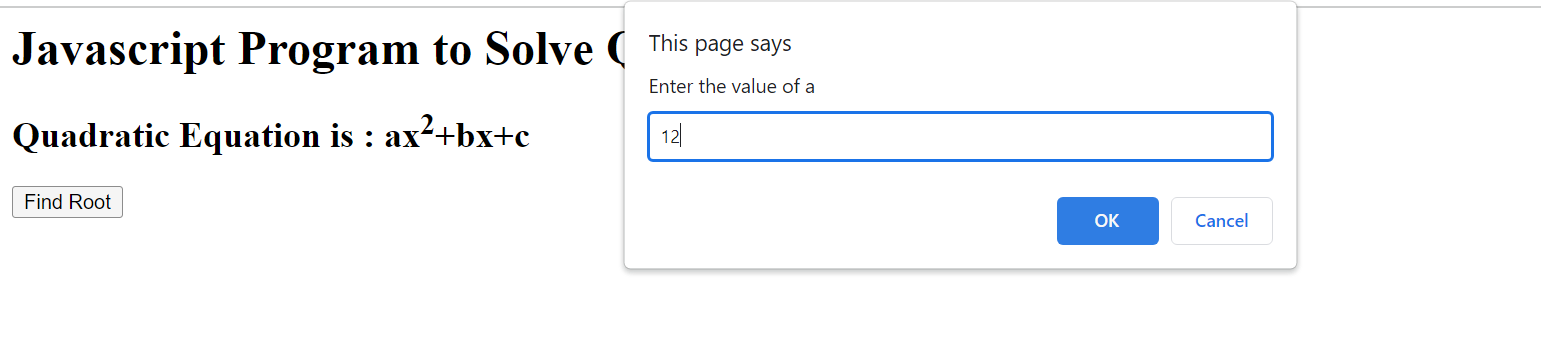
let a = prompt("Enter the value of a");
let b = prompt("Enter the value of b");
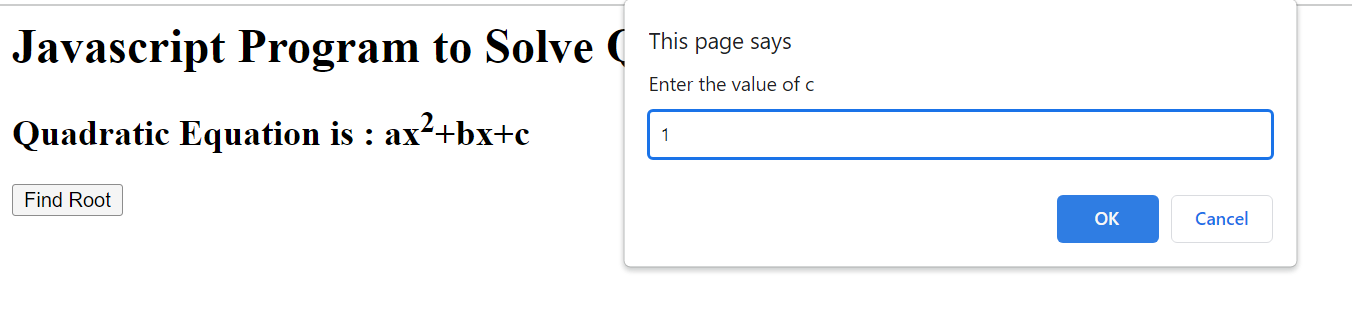
let c = prompt("Enter the value of c");
let discriminant = b*b - 4*a*c;
//(-b ± √b2-4ac)/2
let x = (-b+ Math.sqrt(discriminant))/2;
let y = (-b- Math.sqrt(discriminant))/2;
alert("Your first root is"+x);
alert("your second root is"+y);
}
</script>
</body>
</html>