NumPy is a kind of library that is a part of the Python Programming Language. It adds support for the large, multidimensional arrays and matrices. This is done along with the large collection of the very high-level mathematical functions to operate on these arrays. We use numpy.sort() shortcut to execute the code. This function will return a sorted copy of an array.
About NumPy Sorting
The various sorting algorithms are characterized by the average speed. Sometimes, it also depends on the workspace size and stability. A stable sort of data keeps the items with the same key in the same and relative order. The four algorithms that are implemented in NumPy have the following properties:
| Kind | Speed | Worst Case | Work Space | Stable |
| quicksort | 1 | O(n^2) | 0 | No |
| heapsort | 3 | O(n*(log(n)) | 0 | No |
| mergesort | 3 | O(n*(log(n)) | ~n/2 | Yes |
| timsort | 2 | O(n*(log(n)) | ~n/2 | Yes |
The determination of data types is done on the basis and usage of ‘mergesort’ or ‘timsort’. Also, it can be done if the ‘mergesort’ is specified or not and if the user selection is done at a finer scale is not available. All the sort algorithms make temporary copies of the data when sorted along with any axis except the last one.
The sort order for the complex numbers is called lexicographic. If both the real and the imaginary parts are non-nan then the order is determined by the real parts except when they are equal, in this case, the order is determined by the imaginary parts.
Previous to numpy 1.4.0 sorting real and complex arrays that contained nan values led to very undefined behavior. Therefore, in numpy versions 1.4.0, the nan values are sorted to the end. Here, the extended order is:
- Real: [R, nan]
- Complex: [R+R], nan+Rj, nan+nan]
Here, R is a non-nan real value. The complex values with the same nan placements are sorted according to the non-nan part if it exists. In the new version 1.12.0, the quick sort has been changed into the introsort. When the sorting does not make enough progress it switches to the heapsort. By doing this, it makes quick sort the array O(n*log(n)) in the worst case.
Python Numpy Sorting Example
# importing libraries
import numpy as np
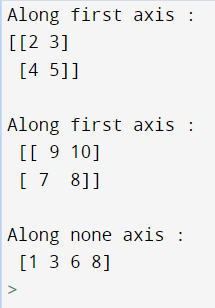
x = np.array([[2, 3], [4, 5]])
arr1 = np.sort(x, axis = 0)
print ("Along first axis : \n", arr1)
x = np.array([[10, 9], [8, 7]])
arr2 = np.sort(x, axis = -1)
print ("\nAlong first axis : \n", arr2)
x = np.array([[3, 6], [8, 1]])
arr1 = np.sort(x, axis = None)
print ("\nAlong none axis : \n", arr1)Output
Open a terminal or command prompt and run the following command :
pip install numpy
The error is occurring because the “numpy” module is not installed. To fix this error, you need to install the NumPy library first. If you are running the code in a local Python environment, you can install NumPy using pip, like this.
After installing NumPy, the code should run without any errors.
The ‘stable’ kind automatically chooses the best stable sorting algorithm for the data type being sorted. ‘Stable’ along with the ‘mergesort’ is currently mapped to the timsort or radix sort. This depends on the data type. API forwards the compatibility that limits the ability to select the implementation and it is hardwired for many different data types.
Latest sorting in new version 1.17.0, Timsort is added for the better performance on already or nearly sorted data. On the random data, timsort is similar to mergesort. The user also uses it for the stable sort, while the quicksort is still the default sort.
Bottom Line
The user can sort data in so many ways in python numpy sorting. But the user prefers the latest version as it gives accurate value and is easy to use.