In this tutorial, we will learn about binary search tree in java. Trees hold immense significance in technical interviews, often occupying a prominent position as one of the most crucial topics. When it comes to software development, the applications of trees surpass those of many other data structures. It makes them indispensable in both the hiring process and actual technical projects. Within the realm of trees, various types exist, but perhaps none are as widely recognized as the binary tree search in java. So, let’s unravel the intricacies of these terms, clarifying each one in turn.

Introduction To Binary Search Tree in Java
A Binary Search Tree (BST), also known as an Ordered Binary Tree. It represents a specific type of binary tree that showcases remarkable characteristics. In this context, BSTs are defined as node-based binary trees. The values of the nodes in the left subtree are consistently smaller than the value of the root node. Conversely, the nodes in the right subtree hold values that exceed that of the root node. This ordering principle extends to the respective subtrees as well, ensuring a cohesive structure throughout the entire BST.
The BST data structure shines in terms of efficiency, particularly when compared to Arrays and Linked Lists. It particularly in operations such as insertion, deletion, and searching for items. Searching for an element in a BST can be accomplished in O(log n) time complexity. The ordered nature of the elements enables a systematic elimination of half the subtree at each step of Binary searching in java. This efficiency stems from our ability to readily determine the approximate location of the desired element within the BST.
Likewise, insertion and deletion operations prove to be highly efficient in a BST. When inserting a new element, we possess a rough understanding of which subtree, either left or right, should house the new node. This knowledge allows us to navigate the BST swiftly, resulting in an expedited insertion process.
Overall, a Binary Search Tree offers a powerful and optimized approach to storing and accessing data, making it an indispensable tool in a wide range of applications. Its innate efficiency, combined with its well-defined ordering principles, makes it an appealing choice for various software development scenarios.
Tree Traversal
When it comes to traversing trees, there are three primary methods that yield distinct node arrangements. Each approach serves a specific purpose and provides us with valuable insights. Let’s delve into each of these traversal techniques:
- Preorder traversal: This method entails printing the root first, followed by recursive function calls for the left subtree and the right subtree. Preorder traversal proves beneficial for tasks like copying the tree’s contents, which can be utilized to construct a prefix expression. This becomes particularly valuable in parsing expression trees, a technique employed by compilers to separate symbols and data within the tree structure.
- Postorder traversal: In this traversal, the function is recursively called for the left subtree and the right subtree before printing the root. Postorder traversal shines when it comes to completely deleting a tree. By deleting the child nodes first and then the root, it ensures the tree is eliminated entirely, from the root down to the leaves.
- Inorder traversal: Among all the traversal techniques, inorder traversal stands out as one of the most widely employed methods. It involves recursive function calls for the left subtree, printing the root, and then recursive function calls for the right subtree. Its primary usage lies in printing all the nodes of the tree in ascending order. Additionally, it can be modified to print the nodes in descending order as well.
These traversals hold significance due to their specific applications and can be implemented effectively using recursive algorithms. If you’re interested in exploring tree traversals in more depth, including practical code examples, we have a comprehensive blog post on tree traversal with recursion that offers detailed insights.
Algorithm for Binary Search Tree in Java
There is an Binary Search Algorithm Tree In java-
public class BinarySearchTree {
private Node root;
private class Node {
int key;
Node left;
Node right;
public Node(int key) {
this.key = key;
left = null;
right = null;
}
}
public BinarySearchTree() {
root = null;
}
public void insert(int key) {
root = insertNode(root, key);
}
private Node insertNode(Node currentNode, int key) {
if (currentNode == null) {
return new Node(key);
}
if (key < currentNode.key) {
currentNode.left = insertNode(currentNode.left, key);
} else if (key > currentNode.key) {
currentNode.right = insertNode(currentNode.right, key);
}
return currentNode;
}
public boolean search(int key) {
return searchNode(root, key);
}
private boolean searchNode(Node currentNode, int key) {
if (currentNode == null) {
return false;
}
if (key == currentNode.key) {
return true;
} else if (key < currentNode.key) {
return searchNode(currentNode.left, key);
} else {
return searchNode(currentNode.right, key);
}
}
public void delete(int key) {
root = deleteNode(root, key);
}
private Node deleteNode(Node currentNode, int key) {
if (currentNode == null) {
return null;
}
if (key < currentNode.key) {
currentNode.left = deleteNode(currentNode.left, key);
} else if (key > currentNode.key) {
currentNode.right = deleteNode(currentNode.right, key);
} else {
if (currentNode.left == null) {
return currentNode.right;
} else if (currentNode.right == null) {
return currentNode.left;
}
currentNode.key = findMinKey(currentNode.right);
currentNode.right = deleteNode(currentNode.right, currentNode.key);
}
return currentNode;
}
private int findMinKey(Node currentNode) {
int minValue = currentNode.key;
while (currentNode.left != null) {
minValue = currentNode.left.key;
currentNode = currentNode.left;
}
return minValue;
}
}
In the code above, we have a BinarySearchTree class that represents a binary search tree. The tree consists of nodes, where each node has a key value, a left child node, and a right child node.
Insertion
The insert method is used to insert a new key into the binary search tree. It starts by calling the private insertNode method, which recursively traverses the tree to find the appropriate position for the new key. If the current node is null, a new node is created with the given key. Otherwise, depending on whether the key is less than or greater than the current node’s key, the method continues traversing the left or right subtree until it finds the appropriate spot.
Deletion
The delete method is used to delete a key from the binary search tree. It calls the private deleteNode method, which recursively searches for the key and deletes it from the tree. If the current node is null, the key is not found and the method returns null. Then If the key is less than the current node’s key, the method continues searching in the left subtree. If the key is greater than the current node’s key, the method continues searching in the right subtree. If the key is equal to the current node’s key, it checks for different cases:
- If the current node has no left child, it returns the right child as the new node.
- If the current node has no right child, it returns the left child as the new node.
- If the current node has both left and right children, it finds the minimum key in the right subtree (the smallest key greater than the current node’s key), replaces the current node’s key with the minimum key, and recursively deletes the minimum key from the right subtree.
Searching
The search method is used to search for a key in the binary search tree. It calls the private searchNode method, which recursively searches for the key in the tree. If the current node is null, the key is not found. If the key is equal to the current node’s key, the method returns true. Otherwise, it continues searching in the left or right subtree based on the key’s value.
Finding Minimum Value
The findMinKey method is a helper method that finds the minimum key in a given subtree by traversing the left children of the subtree until it reaches the leftmost node.
This implementation provides the basic functionality of a binary search tree in Java, allowing you to insert, search, and delete keys efficiently.
Example of Binary Search Tree In Java
public class BinarySearchTree {
private Node root;
private class Node {
int key;
Node left;
Node right;
public Node(int key) {
this.key = key;
left = null;
right = null;
}
}
public BinarySearchTree() {
root = null;
}
public void insert(int key) {
root = insertNode(root, key);
}
private Node insertNode(Node currentNode, int key) {
if (currentNode == null) {
return new Node(key);
}
if (key < currentNode.key) {
currentNode.left = insertNode(currentNode.left, key);
} else if (key > currentNode.key) {
currentNode.right = insertNode(currentNode.right, key);
}
return currentNode;
}
public boolean search(int key) {
return searchNode(root, key);
}
private boolean searchNode(Node currentNode, int key) {
if (currentNode == null) {
return false;
}
if (key == currentNode.key) {
return true;
} else if (key < currentNode.key) {
return searchNode(currentNode.left, key);
} else {
return searchNode(currentNode.right, key);
}
}
public void delete(int key) {
root = deleteNode(root, key);
}
private Node deleteNode(Node currentNode, int key) {
if (currentNode == null) {
return null;
}
if (key < currentNode.key) {
currentNode.left = deleteNode(currentNode.left, key);
} else if (key > currentNode.key) {
currentNode.right = deleteNode(currentNode.right, key);
} else {
if (currentNode.left == null) {
return currentNode.right;
} else if (currentNode.right == null) {
return currentNode.left;
}
currentNode.key = findMinKey(currentNode.right);
currentNode.right = deleteNode(currentNode.right, currentNode.key);
}
return currentNode;
}
private int findMinKey(Node currentNode) {
int minValue = currentNode.key;
while (currentNode.left != null) {
minValue = currentNode.left.key;
currentNode = currentNode.left;
}
return minValue;
}
public void printInOrder() {
System.out.print("In-order traversal: ");
printInOrder(root);
System.out.println();
}
private void printInOrder(Node currentNode) {
if (currentNode != null) {
printInOrder(currentNode.left);
System.out.print(currentNode.key + " ");
printInOrder(currentNode.right);
}
}
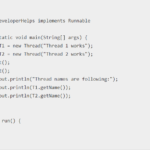
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
// Inserting values into the binary search tree
bst.insert(50);
bst.insert(30);
bst.insert(20);
bst.insert(40);
bst.insert(70);
bst.insert(60);
bst.insert(80);
// Printing the in-order traversal of the tree
bst.printInOrder();
// Searching for a key
int searchKey = 40;
if (bst.search(searchKey)) {
System.out.println(searchKey + " found in the tree.");
} else {
System.out.println(searchKey + " not found in the tree.");
}
// Deleting a key
int deleteKey = 30;
bst.delete(deleteKey);
System.out.println("After deleting " + deleteKey + " ");
bst.printInOrder();
}
}
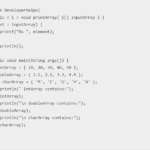
In this code, we create a BinarySearchTree class that represents a binary search tree. The program demonstrates the usage of the tree by inserting values (50, 30, 20, 40, 70, 60, 80), performing an in-order traversal, searching for a key (40), and deleting a key (30).
When you run the program, it will output the in-order traversal of the tree, search for the specified key, and then delete the specified key. Finally, it will print the updated in-order traversal of the tree.
Output :
In-order traversal: 20 30 40 50 60 70 80
40 found in the tree.
After deleting 30
In-order traversal: 20 40 50 60 70 80Follow for More Info – https://instagram.com/developerhelps?igshid=MzRlODBiNWFlZA==